jaescape.blogg.se

The word "MOI" stands for Moment of Inertia. Solve for the moment of inertia using the transfer formula. We found that the moment of inertia when the rod rotates about a parallel axis passing through the end of the rod is: What is the moment of inertia I com for a uniform rod of length L and mass M rotating about an axis through the center, perpendicular to the rod? Let's use it to go the other way, using the moment of inertia we just calculated for a rod rotating about one end. The parallel-axis theorem is usually used to calculate the moment of inertia about a second axis when I com is known. Where h is the distance from the center-of-mass to the current axis of rotation, and I com is the moment of inertia for the object rotating about the axis through the center of mass that is parallel to the current axis. The moment of inertia increases as the rotation axis is moved further from the center-of-mass.įor an object of mass M, the parallel-axis theorem states:

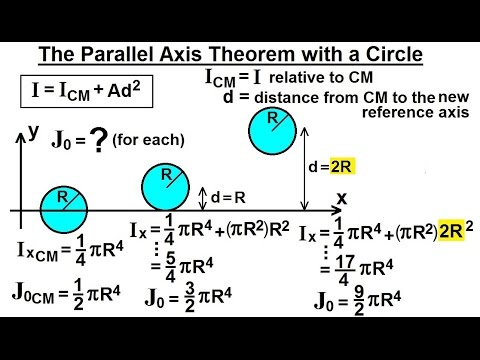
It's easier to look up the result in the table on page 227 in the book.įor a given rotation axis direction, the moment of inertia will always be minimized when the axis of rotation passes through the object's center-of-mass.

We could carry out such integrals for all sorts of different shapes, although many of them are inetgrals over areas or volumes instead of over lengths. X 3] with upper limit L and lower limit 0įor a uniform rod rotating about one end.

Split the rod into little pieces of size dx. How do we evaluate the moment of inertia integral:įor a uniform rod of length L rotating about an axis passing through one end of the rod, perpendicular to the rod?Īlign the rod with the x axis so it extends from 0 to L. The moment of inertia, I, is the rotational equivalent of mass.įor a simple object like a ball on a string being whirled in a circle, where all the mass can be considered to be the same distance away from the axis of rotation, the moment of inertia is:įor something more complicated, where mass is distributed at different distances from the rotation axis, the moment of inertia is determined by integrating:Įxample - a uniform rod of length L rotating about one end